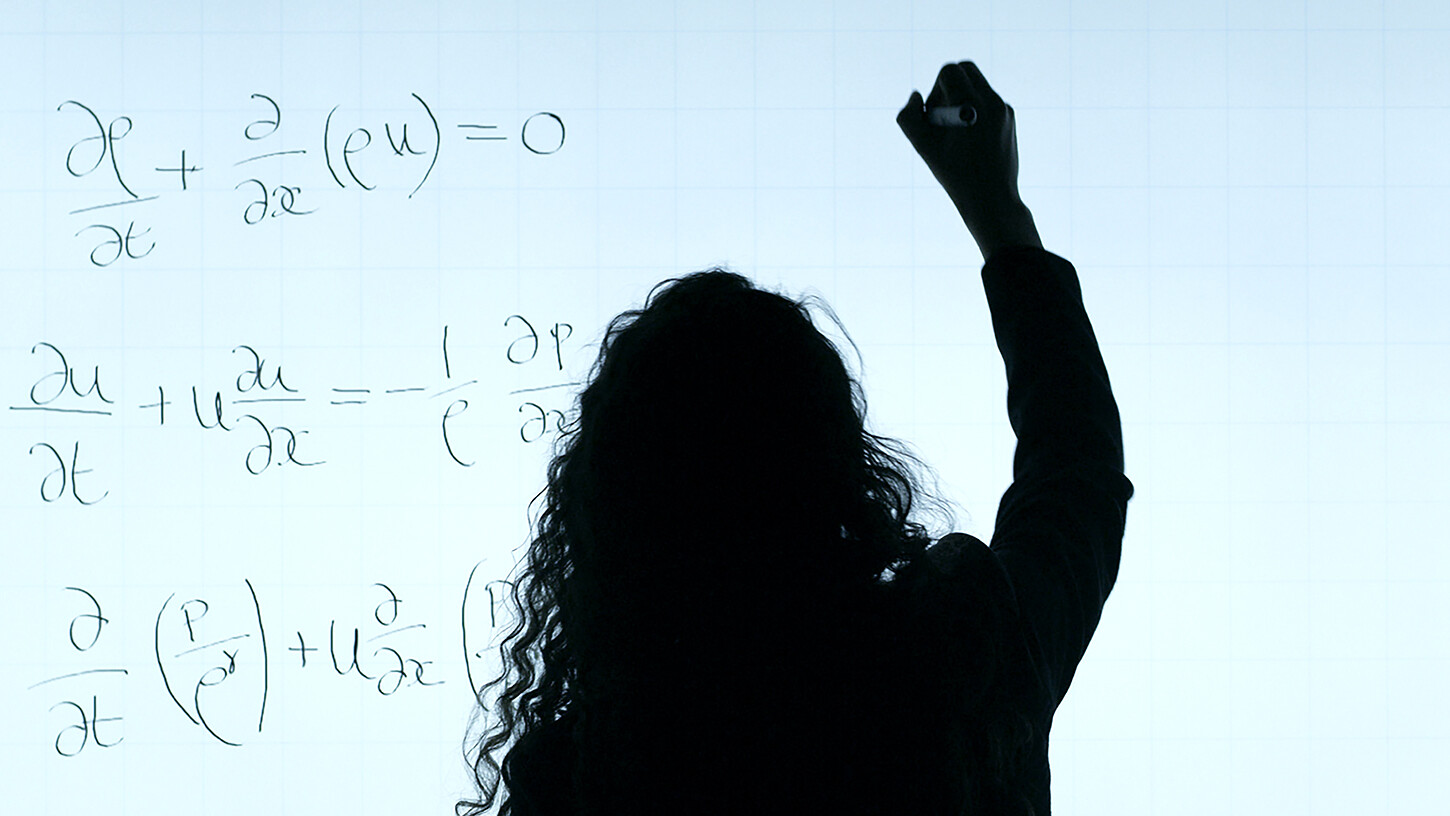Warum es so schwer ist, die Verbreitung von COVID-19 zu modellieren

„Die Datenlage ist bei neuen Erregern nicht gut, weil zu wenig über sie bekannt ist“, sagt Marie-Therese Wolfram. Deswegen seien Modellierungen der Pandemie mit Vorsicht zu genießen. Dennoch hätten diese Modelle im Kampf gegen die Ausbreitung des Coronavirus ihre Berechtigung, denn: „Die Modelle können ja ständig verbessert werden und je länger der Beobachtungszeitraum wird, desto besser werden auch die Daten“, so die Mathematikerin, die an der University of Warwick und der Österreichischen Akademie der Wissenschaften (ÖAW) forscht.

Im Interview spricht sie darüber, welche Methoden die Mathematik aktuell anwendet, um die Pandemie zu modellieren, warum großflächige Antikörpertests die Datenlage verbessern würden und weshalb Boris Johnson - mathematisch betrachtet - manchmal Äpfel mit Birnen vergleicht.

Auf welchem Gebiet forschen Sie?

Marie-Therese Wolfram: Ich entwickle Modelle, die das Verhalten von Populationen, etwa Tieren, Zellen oder Menschenmassen beschreiben. Dabei setzen wir auf Systeme aus partiellen Differentialgleichungen, die auch bei Corona-Modellen zum Einsatz kommen. Dieser Ansatz hat den Vorteil, dass er auch für analytische Methoden zugänglich ist. Die Ausbreitung eines Virus kann durch verschiedene Formen von Exponentialfunktionen beschrieben werden. Haben diese einen positiven Exponenten, wachsen die Fallzahlen, ist er negativ, flacht die Kurve ab.

Was macht es so schwierig, eine neuartige Viruserkrankung wie COVID-19 zu modellieren?

Wolfram: Grundsätzlich ist schon die Identifizierung des passenden Modells schwierig. Es gibt eine große Zahl von Möglichkeiten. Welches Modell gewählt wird, hängt von der Fragestellung ab. Eine Gemeinsamkeit aller Modelle ist, dass sie zeitabhängig sind und somit eine Entwicklung der Fallzahlen beschrieben. Das heißt, ich benötige sowohl einen Startwert – also die Anzahl gesunder nicht-immuner, infizierter, und immuner Personen zum jetzigen Zeitpunkt – als auch Parameter, wie etwa die Ansteckungsrate, um diese Modelle zu simulieren. Die Datenlage ist bei neuen Erregern aber nicht gut, weil zu wenig über sie bekannt ist. Das bedeutet, die Anfangsbedingungen als auch die Parameter sind mehr oder weniger gut geschätzt - die Vorhersagen der Modelle können in beide Richtungen abweichen.

Bei Krankheitsmodellen ist gerade Langzeitverhalten interessant. Flacht die Kurve ab oder wächst sie an? Da können mathematische Analysen sehr hilfreich sein.

Liefert die Modellierung unter diesen Bedingungen überhaupt belastbare Prognosen?

Wolfram: Wie immer sind jegliche Prognosen mit Vorsicht zu geniessen, aber mathematische Modellierung hat ihren Stellenwert. Die Modelle können ja ständig verbessert werden und je länger der Beobachtungszeitraum wird, desto besser werden auch die Daten. Das passiert derzeit auch. Kolleg/innen am Imperial College in London haben ihre Prognosen bereits mehrfach verbessert und revidiert, einfach weil sie bessere Informationen über die Übertragungsraten für verschiedene Berufs- oder Altersgruppen zur Verfügung hatten.

Welche Methoden zur Modellierung werden üblicherweise genutzt?

Wolfram: Die Bevölkerung wird normalerweise in infizierte, anfällige und bereits genesene Personen unterteilt. Diese SIR-Modelle (Susceptible, Infected, Recovered, Anm.) werden mit Grundannahmen über die Verbreitung des Virus gefüttert. Daraus lassen sich verschiedene Systeme von Differentialgleichungen erstellen – deren Bausteine sind relativ simpel, in ihren verschiedenen Kombinationen dann allerdings oft komplex. Die Lösungen dieser Systeme liefern dann Zahlen, welche Auskunft über die Menge an infizierten oder immunen Personen geben. Es gibt verschiedenste Varianten dieser SIR-Modelle, die etwa verschiedene Infektionsstadien berücksichtigen können.

Die Konfidenzintervalle, mit denen Wissenschaftler/innen ihre Prognosen versehen, werden von der Politik meistens unter den Teppich gekehrt.

Ein zweiter Ansatz sind agentenbasierte SIR-Modelle. Dabei werden einzelne Personen und ihre Interaktionen simuliert. Die sind für Mathematiker/innen aber eher ein Graus, weil analytische Ansätze hier nicht mehr anwendbar sind. Die Modelle sind zu komplex – die Anzahl der Akteure und Interaktionen zu groß. Aber auch diese Modelle haben ihren Stellenwert – Aussagen basieren hier allerdings meist nur auf Computersimulationen.

Was können Mathematiker/innen durch die Analyse der gleichungsbasierten Modelle lernen?

Wolfram: Bei Krankheitsmodellen ist gerade Langzeitverhalten interessant. Flacht die Kurve ab oder wächst sie an? Da können mathematische Analysen sehr hilfreich sein. Die sind bei agentenbasierten Computermodellen wesentlich schwieriger – man versucht dort eher den Ausgang für verschiedenste Szenarien (Anfangsbedingungen, Ansteckungsraten) durchzuspielen. Gesichert sind diese Aussagen allerdings nicht – man weiss nicht, was passiert, wenn man einen Parameter etwas ändert. Welcher der beiden Ansätze gewählt wird, hängt schlicht von der Fragestellung ab. 

Die Zahl der Infizierten wächst ja anfangs exponentiell, flacht dann aber oft ab, um eventuell später wieder zu steigen - Stichwort zweite Welle. Wie spiegelt sich dieses Verhalten in mathematischen Modellen wieder?

Wolfram: Die Anzahl an Infizierten kann nicht immer exponentiell wachsen, dieses Wachstum wäre spätestens mit der Ausrottung des Wirts vorbei. Klassische SIR-Modelle haben deshalb kein durchgehendes exponentielles Wachstum. Aber es kann auch in Varianten dieser Modelle beobachtet werden, dass die Kurve nach einem zwischenzeitlichen Abflachen wieder stark ansteigt. Die aktuelle globale Dynamik und die Zeitskalen machen die Modellierung nochmals komplizierter. Auch saisonale Schwankungen in der Ausbreitung können das Wachstum beeinflussen. Da die Lösungen oft exponentieller Natur sind, wachsen auch Fehler aufgrund falscher Annahmen oder Parameter entsprechend schnell. Deshalb sind Langzeitprognosen mit Vorsicht zu genießen. Hier tragen die Modellierenden besondere Verantwortung.

Die Politik hat ihre Entscheidungen oft mit Modellen unterfüttert. Ist das bei den vielen Unsicherheiten klug?

Wolfram: Politiker/innen haben viele ihrer Aussagen mit wissenschaftlichen Prognosen begründet. Das ist grundsätzlich sehr begrüßenswert, nur muss bedacht werden, wie Kommunikation in diesem Zusammenhang funktioniert. Die Konfidenzintervalle, mit denen Wissenschaftler/innen ihre Prognosen versehen, werden von der Politik meistens unter den Teppich gekehrt. Boris Johnson hat erst vor kurzem versucht, seine politischen Entscheidungen mithilfe einer Gleichung zu untermauern. Dabei wurde er aber anscheinend schlecht beraten. Die Gleichung machte absolut keinen Sinn - er hat quasi Äpfel mit Birnen verglichen.

Je länger die Pandemie dauert, desto besser werden die Daten. Wirkt sich das auf die Modelle aus?

Wolfram: Großflächige Antikörpertests wären ein enormer Fortschritt. Dann hätten wir belastbare Daten und könnten damit die Modelle verbessern. Denn letztendlich kann man fast jedes Modell mit einem einzelnen Datensatz „fitten“ – nur ist das dann für diesen Datensatz spezifisch. Gute Modelle liefern weiterhin valide Aussagen, wenn man Anfangsbedingungen etwas ändert beziehungsweise langfristige Prognosen erstellt. Für die Grippe zum Beispiel, die schon lange erforscht wird, haben wir sehr gute Modelle.

Die Komplexität unserer Gesellschaft, die globale als auch lokale Dynamik, sind extrem schwer zu erfassen.

Erlauben die COVID-19-Modelle Aussagen über die Wirksamkeit von Maßnahmen der Regierung zur Verhinderung der Ausbreitung?

Wolfram: Ja – in einem gewissen Rahmen. Ein kompletter Lockdown könnte zum Beispiel dadurch modelliert werden, dass man Interaktionsparameter auf 0 setzt. Dann kann man vergleichen, wie sich unterschiedliche Werte auf das Verhalten der Ansteckungskurve auswirken. Aber letztendlich ist das alles nicht leicht quantifizierbar. Handydaten liefern zum Beispiel Anhaltspunkte über die Reduktion der sozialen Kontakte, aber dies sind auch nur Schätzungen. Nehme ich also eine 30- oder 50-prozentige Reduktion der Kontakte an? Regierungen haben das sicher durchrechnen lassen, aber auch hier sind Annahmen im Spiel.

Das heißt dass neben dem Virus auch Menschen unberechenbar sind?

Wolfram: Natürlich, gerade in unserer heutigen Gesellschaft. Politiker/innen würden gerne wissen, um wie viel sie die Interaktion verringern müssen, um die Verbreitungskurve abzuflachen. Aber die Komplexität unserer Gesellschaft, die globale als auch lokale Dynamik, sind extrem schwer zu erfassen. Ich selbst reise normalerweise ständig zwischen England und Österreich hin und her – es wäre ein leichtes gewesen, den Virus aus London „mitzubringen“. Herauszufinden, wie man diese räumlichen und zeitlichen Skalen korrekt berücksichtigt, ist eine riesige Herausforderung für die Modelle.